When we hear the words “Nuclear Magnetic Resonance” (NMR) what first comes to our minds is probably those huge and noise machines in hospitals. However, much more than that, NMR is a powerful technique that helps us to understand how the microscopic world arranges itself, and its applications extend to many different areas in chemistry, physics, biology… In this post, I will briefly explain the principles behind this technique and how it is applied to quantum information studies.
In the same way that any physical body has “mass” as an intrinsic property and this mass interacts with Earth’s gravitational force, some nuclei (like hydrogen, nitrogen…) have also an intrinsic “nuclear spin”. This spin allows those particles to feel and respond when a magnetic field is present. Like a compass that will orient itself according to Earth’s magnetic field, the nuclear spins will follow the local magnetic field around its position.
interacts with Earth’s gravitational force, some nuclei (like hydrogen, nitrogen…) have also an intrinsic “nuclear spin”. This spin allows those particles to feel and respond when a magnetic field is present. Like a compass that will orient itself according to Earth’s magnetic field, the nuclear spins will follow the local magnetic field around its position.
So, imagine that you have a set of very small magnets spread on a table, like people on a dancing floor. If you apply a magnetic field and slowly change it, you can make them move as you wish… as in a choreographic dancing!

However, as one person prefers some kinds of music and will dance to some beat more enthusiastically than to others, different nuclear spin species have particular frequency preferences (called Larmour frequencies). In a NMR experiment, we first apply a strong static magnetic field (B0) which defines a reference for our “spin-ballerinas”. Then, we apply a second oscillatory magnetic field (a radio frequency pulse) which has a specific frequency that will only be heard and followed by spins with a preference for this frequency. This phenomenon is called resonance, and is the basis for NMR experiments.
Now, you are probably wondering “If this is all microscopic, how are you able to observe this spin-dancing thing”? And “how is it important for science”?
In 1831, the English scientist Michael Faraday observed the electromagnetic induction principle according to which, when a magnet is moved through a loop of wire, an electric current flow in that wire. So applying this principle, we are able to transform the magnetic “spin dancing” (which is nothing else then a variable magnetic field) into a detectable signal. The result is a signal that oscillates in time. Apparently this signal does not say much, however, if we apply a mathematical transformation that drives 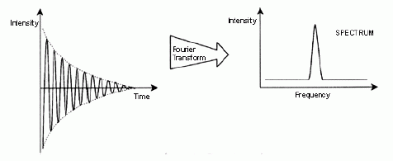 us from time to frequency domain (Fourier transformation) then we can see peaks in some special frequencies: the “special characteristic frequency” of each nucleus! Therefore, when we see a peak on that frequency, we can guarantee that this nucleus is present on our sample.
us from time to frequency domain (Fourier transformation) then we can see peaks in some special frequencies: the “special characteristic frequency” of each nucleus! Therefore, when we see a peak on that frequency, we can guarantee that this nucleus is present on our sample.
Things can get much more interesting than that! In a ball, you (hopefully!) do not need to dance alone all the time, so also nuclear spins can dance (interact) with others. Those interactions will than change our signal and the peaks shape, allowing us to predict who is interacting with whom and in which way. This is why NMR is applied to determine molecular structures so often.

Typical spectra observed in solid state NMR for (a) cubic, (b) axial, (c) non-axial symmetries; (d) Dipolar interaction between two spins 1/2 (I and S); Quadrupolar interaction for spins (e) 1 and (f) 3/2. (This picture is from the book: NMR Quantum Information Processing. I.S.Oliveira (2007) Elsevier.)
But this is a quantum information blog… what all this “dancing” stuff has to do with it? Classical computers (the ones we have in our houses) are built to process information based on bits. So everything that happens inside is described by a code with combinations of 0s and 1s. In this case you only have two options… either your bit is 0 or it is 1, like when you throw a coin and it gives you head or tail. In an electrical circuit, we can translate this for “you have” (bit 1) or “you have not” (bit 0) an electrical signal. But… what if you could have both options? Would it change the way the information is processed? Would it make computers faster? That is exactly what we are investigating nowadays.
Coming back to our dancing spins… Relatively to our reference magnetic field, a spin can b e in a parallel (associated to bit 0) or an anti-parallel (associated to bit 1) position, however our spins can also lie on the perpendicular plane, which corresponds to a “superposition state” (a combination of 0 and 1 at the same time). In this sense, we can apply NMR as a “quantum computer simulator” where we will encode bits as qubits (quantum-bits), and denote them by |0> and |1>.
e in a parallel (associated to bit 0) or an anti-parallel (associated to bit 1) position, however our spins can also lie on the perpendicular plane, which corresponds to a “superposition state” (a combination of 0 and 1 at the same time). In this sense, we can apply NMR as a “quantum computer simulator” where we will encode bits as qubits (quantum-bits), and denote them by |0> and |1>.
To exemplify how powerful quantum algorithms can be, I propose the following game. Suppose you have four balls numbered sequentially {1, 2, 3, 4}. I will cover the numbers and mix them cyclically. The possible outcomes are identified below and can be split in two groups: when an even and when an odd permutation – function fi(x) – is applied.

My question for you is “which kind of permutation was performed (even or odd)”? You can guess and will have 50% chance to answer correctly, but to be sure you would need to uncover at least two balls. To answer a question like that: “which parity a certain function has?” a classical computer would need to evaluate it at least two times. However, applying a quantum algorithm we proved that it is possible to answer that question looking only at a single result.
Our system was a liquid crystal containing a 23Na nucleus. In a first step, we apply some radiofrequency pulses to prepare our spin system in a pre-determined configuration |ψ>. Then, we apply three functions sequentially… a quantum Fourier transformation (UFT), the fi(x) chosen randomly, and the inversion form of this quantum Fourier transformation (UFT†). The result is such that: if after applying those three functions our spin is in the same configuration as in the beginning, then the fi(x) permutation was even, otherwise it was odd…and the function fi(x) was evaluated only once! This makes our “quantum computer” two times faster than a classical computer when evaluating the same problem.

Many other interesting quantum properties, like quantum correlations (mentioned by my colleagues before) – where we need to explore the interactions between different spin nuclei – can be also simulated using NMR setups. But this is a topic for another time…
Pingback: Can we freeze something at room temperature? Yes, quantum coherence! | quanta rei